저번 포스팅에서 부울 대수가 무엇인지 알아보고 부울 대수를 사용해 논리식을 간소화 할 수 있다는 것을 알아보았습니다. 이번 포스팅에서는 Minterm과 Maxterm이 무엇인지 알아보고 다양한 Logic Gate들에 대해 알아보겠습니다.

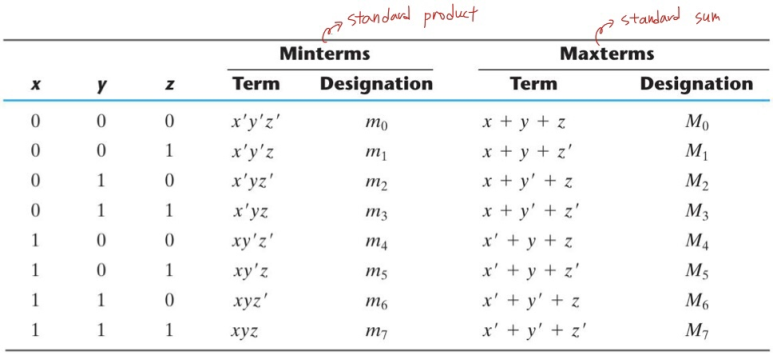
위 표에서 **모든 input case들에 대해 0이면 complementary로 쓰고 1값이면 그대로 써줘 곱하기로 연결한 것을 Minterms(= standard product)**라고 합니다. 반대로 **모든 input case들에 대해 0이면 그대로 써주고 1값이면 complementary를 사용해 써줘 더하기로 연결한 것을 Maxterms(= standard sum)**이라고 합니다. 이때 표를 보면 Minterm과 Maxterm은 서로 complementary 관계인 것을 알 수 있습니다.

이렇게 Minterm과 Maxterm을 이용해 우리는 Boolean Function을 표현할 수 있습니다.

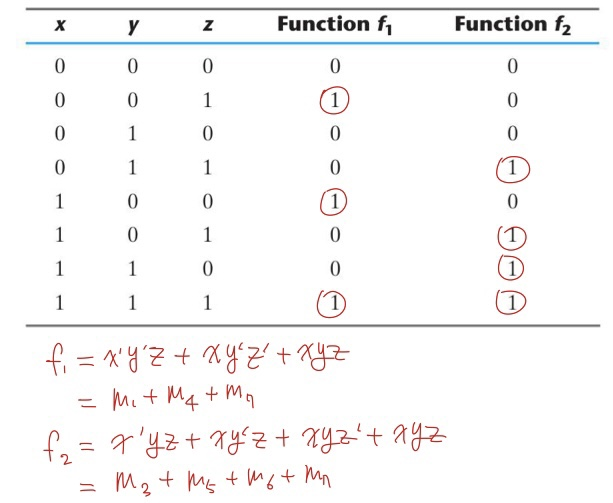
f1과 f2를 Minterm으로 나타내면 위와 같습니다. 그렇다면 f1과 f2의 complementary는 언제 1이 될까요? 바로 f1과 f2이 0이 될때 complementary는 1이 됩니다.

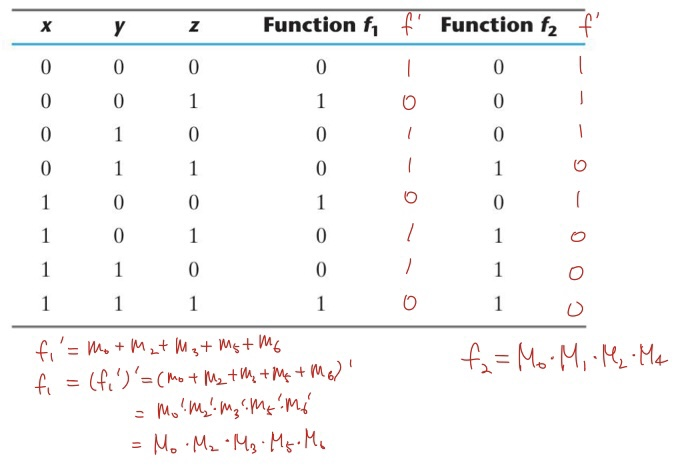
이것을 Maxterm으로 나타내면 위와 같이 표현할 수 있습니다. 이때 Boolean Function을 Minterm들의 Sum 혹은 Maxterm들의 Product로 나타낸 것을 Canonical Form으로 나타냈다고 합니다. 다음은 주어진 Boolean Function을 Minterm의 sum으로 표현하는 예제를 보도록 하겠습니다.

위와 같이 부울 대수를 사용해 F = A + B'C를 sum of minterms로 나타낼 수 있습니다. 다음은 주어진 Boolean Function을 Maxterm의 product으로 표현하는 예제를 보도록 하겠습니다.

F = xy + x'z를 부울 대수를 사용해 product of maxterms로 나타낼 수 있습니다.

위 문제를 보면 알 수 있듯이 Minterm은 Boolean Function이 0값을 가질 때 Maxterm은 Boolean Function이 1값을 가질 때를 집중해서 보면 되는 것을 알 수 있습니다.

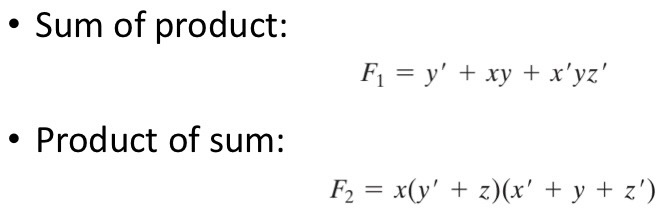
다음은 Standard Form에 대해 알아보도록 하겠습니다. 위에 나와있는 Sum of product와 Product of sum를 우리는 Standard Form이라고 합니다.

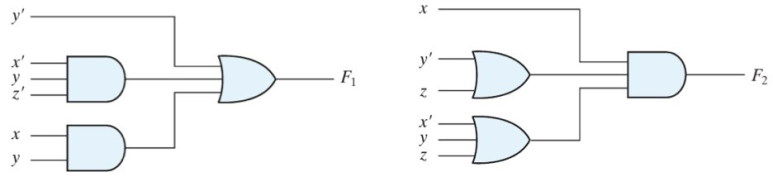
그리고 Standard Form을 two-level structure of gates로 표현할 수 있습니다.