저번 포스팅에서 Minterm/Maxterm에 대해 알아보고 sum of product와 product of sum에 대해 알아보았습니다. 그리고 AND/OR/NOT 외에 다양한 Logic Gate에 대해서 알아보았는데 이번 포스팅에서는 K-Map에 대해서 알아보고 K-Map을 사용해 Gate-Level Minimization까지 해보도록 하겠습니다.
그렇다면 Two Variable K-Map부터 자세하게 알아보겠습니다.

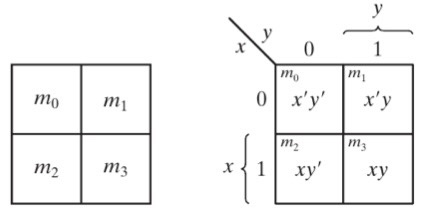
2 input에 대해 K-Map은 위와 같이 그릴 수 있습니다. 이때 K-Map 안에는 Minterm에 들어가는 것을 알 수 있습니다. 위 사진은 K-Map 안에 Minterm 값이 들어간다는 것을 표현하기 위해 나타낸 것입니다. K-Map 안에는 Minterm 즉 Function이 1이 될 때를 표시하면 됩니다.
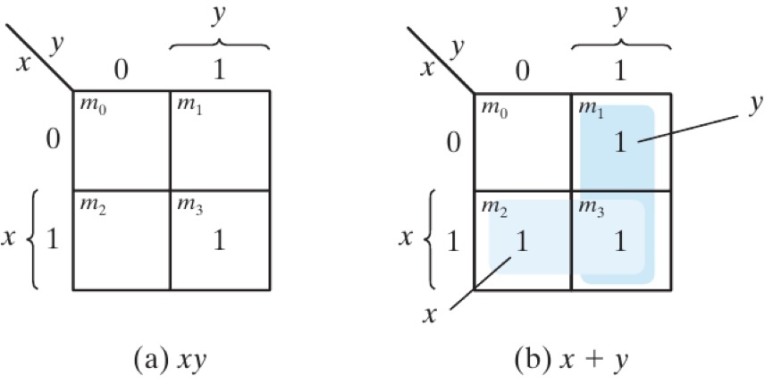
xy와 x + y 에 대해 K-Map을 그려보면 위와 같이 나오게 됩니다. 그렇다면 Three Variable K-Map은 어떻게 그리면 될까요?
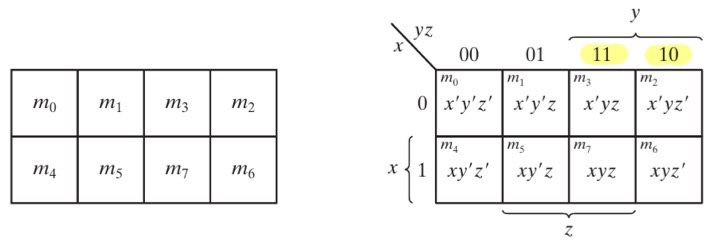
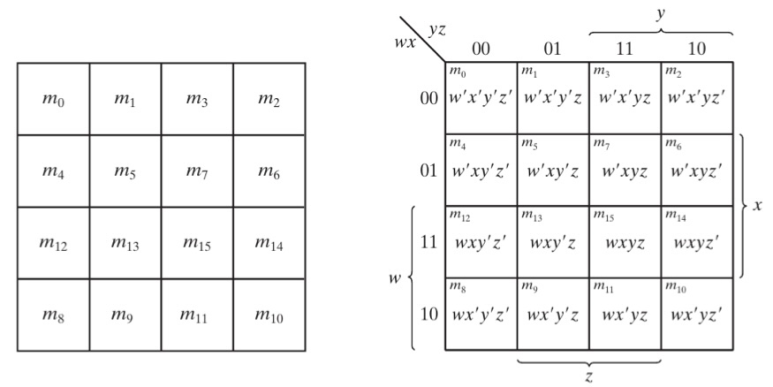
Three Variable K-Map은 위와 같이 표현됩니다. yz는 00 01 11 10 순서가 아닌 00 01 11 10 순서로 표시되었는데 이는 코드가 하나씩 바뀔때마다 1 bit씩 변하는 Gray Code를 사용했음을 알 수 있습니다.
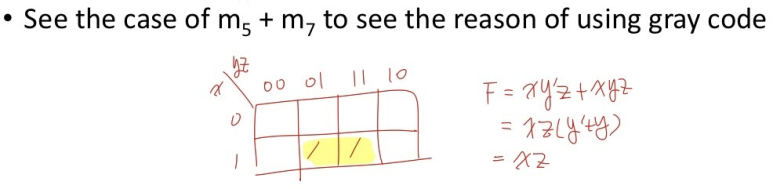
m5 + m7 을 K-Map을 사용해 표현하면 위와 같이 나타낼 수 있습니다. K-Map을 통해 Boolean Function을 구하려면 1을 포함한 사각형을 제일 크게 그리면 됩니다. 이게 무슨 말인지 알아보겠습니다.
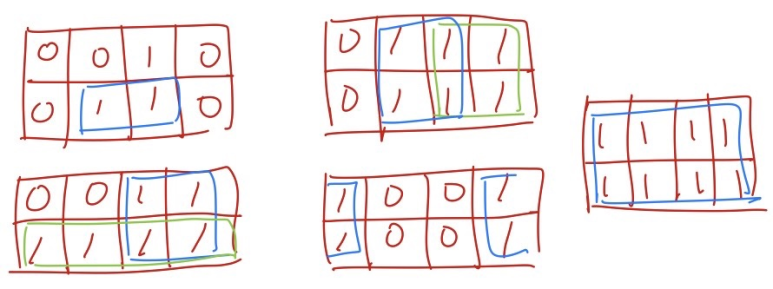
Three Variable K-Map에 대해 위와 같이 나타낼 수 있습니다. 이렇게 사각형을 그리면 해당 사각형은 어떤 하나의 Term에 해당합니다. 위에서 그린 m5 + m7 은 xz Term인 것을 알 수 있습니다. 이때까지 K-Map에 대해 알아보았는데 그렇다면 문제를 풀면서 더 자세하게 알아보겠습니다.
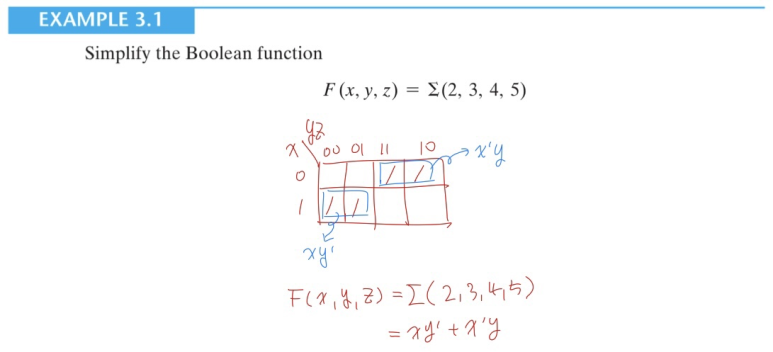
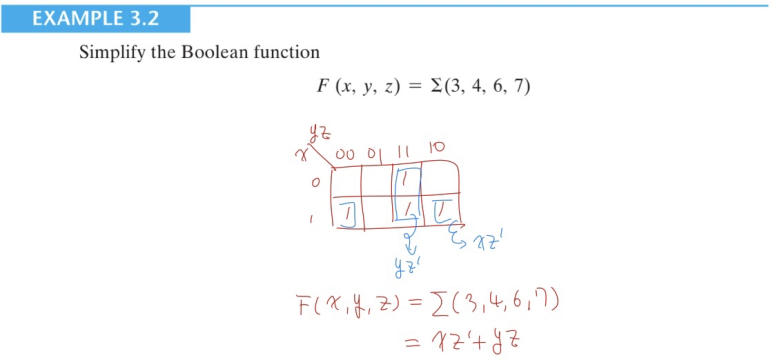
Three Variable K-Map을 통해 Boolean Function을 위와 같이 간소화 할 수 있습니다.

위 문제는 Truth Table를 통해 sum of minterms를 구하고 이를 K-Map을 사용하여 간단하게 표현했습니다. 이때까지 Three Variable K-Map에 대해 알아보았는데 Four Variable K-Map에 대해서도 알아보겠습니다.