저번 포스팅에서 Binary Adder에 대해 알아보았다면 이번 포스팅에서는 Decimal Adder를 구현해보겠습니다.
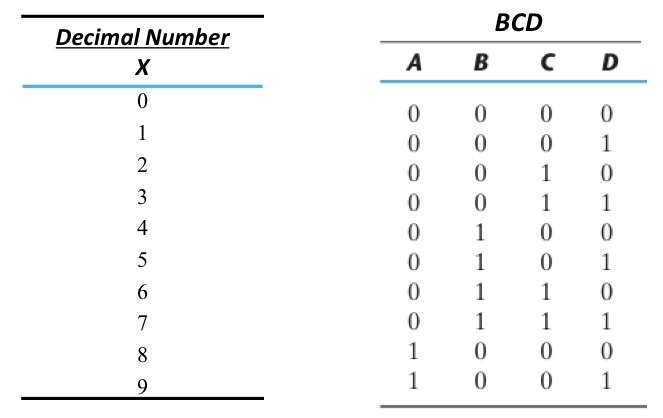
우리가 사용하는 10진수를 컴퓨터가 알아 들을 수 있게 2진수로 표현하려고 하면 몇 bit가 필요할까요? 0~9까지 총 10가지이므로 4bit이 필요하다고 이야기 할 수 있습니다.

기존에 사용하던 10진수를 BCD로 표현하면 위와 같습니다. 그렇다면 Multiple Digit을 표현하려고 하면 어떻게 해야할까요? 10진수 25를 BCD로 표현하면 어떻게 되는지 알아보겠습니다. 2는 BCD로 0010이고 5는 BCD로 0101이므로 25를 BCD로 표현하면 00100101이 됩니다.
1875 + 298 을 생각해보면 둘째 자리에 있는 7과 9를 더할때 우리는 LSB에서 넘어온 Cin에 7과 9를 더해 Sum과 Cout을 내보내는 것을 알 수 있습니다. 지금부터 이런 10진수를 더할 수 있는 BCD Adder를 구현해보려고 합니다.
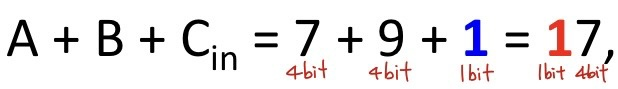
A, B는 4bit BCD 코드로 나타내고 Cin은 1bit으로 표현하는 BCD Adder를 구현해보겠습니다.
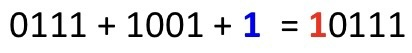
즉 컴퓨터가 위 과정을 수행할 수 있게 회로를 설계해야 합니다.
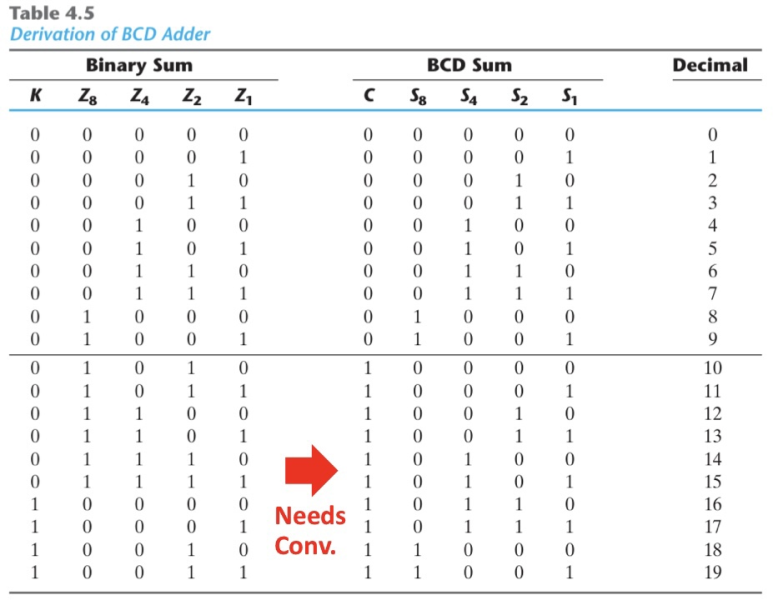
4bit Binary Sum과 BCD sum을 비교한 Table을 보면 위와 같습니다. Table에서 0~9에 대해서는 Binary Sum과 BCD sum이 같으므로 Binary Add를 그대로 사용하고 10~19에 대해서만 Conversion을 진행하는 방법으로 접근을 해보려고 합니다. 그렇다면 어떤 경우에 Conversion을 해야할까요?
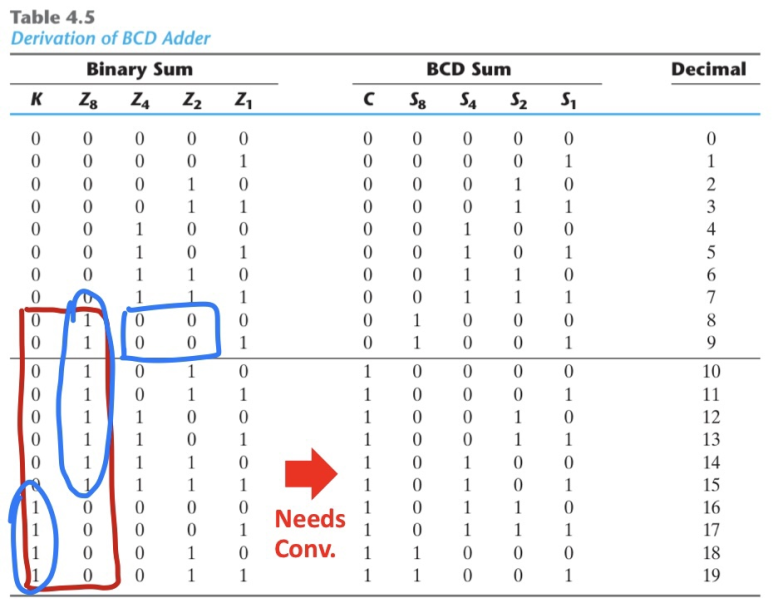
우선 K가 1이라면 Conversion이 무조건 필요한 것을 알 수 있습니다. 하지만 Z8이 1인 경우 10진수 8, 9에 대해서 예외적으로 Conversion이 필요없는 것을 알 수 있습니다. Z8이 1인경우 Conversion이 필요한 case와 필요없는 case를 비교해보면 Z8이 1일때 Z4와 Z2가 모두 0인 case에 대해 Conversion이 필요없다는 것을 Table을 통해 알 수 있습니다.
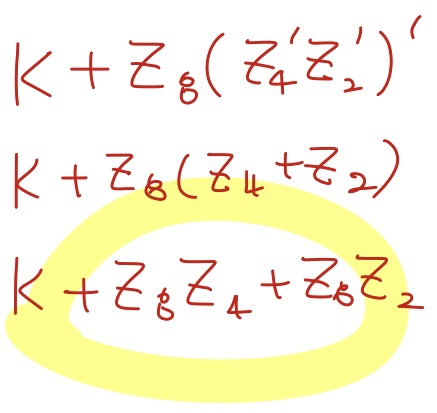
위에서 빨간색으로 표현한 Conversion이 필요한 조건을 논리식으로 나타내면 위와 같이 나오게 됩니다. 즉 BCD Adder은 Binary Adder를 사용하되 위 case의 경우 Conversion이 필요하다는 것 입니다.
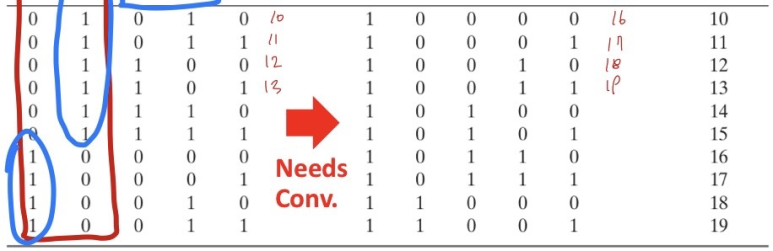
그리고 Conversion된 값과 Binary Sum값을 비교하면 6차이가 나기 때문에 Conversion이 필요한 case에서는 6(0110)을 더해 Conversion을 하여 회로를 구현할 수 있습니다.