저번 포스팅에서 우리는 K-Map을 사용해 Gate Level Minimization을 해보고 다양한 Logic Gate를 구현하는 방법에 대해 알아보았습니다. 이번 포스팅에서는 Combinational Logic에 개념에 대해 알아보고 간단한 binary adder을 구현해보겠습니다.

디지털 회로에는 두 가지가 있는데 하나는 Combinational Logic이고 하나는 Sequential Logic입니다. 이번 포스팅에서는 그 중 하나인 Combinational Logic에 대해 자세하게 알아보려고 합니다.

Combinational circuit는 output이 현재 input에 의해서만 결정되는 회로입니다.

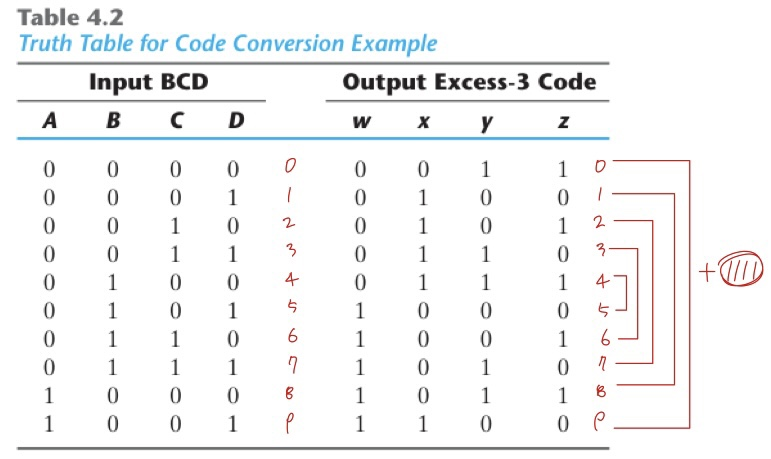
그렇다면 바로 예제를 보면서 Combinational Logic에 대해 알아보겠습니다. 아래 회로는 BCD to Excess-3의 Truth Table입니다.

Input으로 BCD 코드가 들어오면 output은 3을 더해 출력하는 Excess-3 코드입니다. Excess-3 코드를 왜 사용하는지 간단하게 알아보면 위 코드의 bit을 반전시킬 경우 보수값이 나오는 성질이 있습니다. 즉 0을 반전시키면 9가 나오고 1을 반전시키면 8이 나옵니다. 이런 성질 때문에 산술 연산을 할때 편리해 자주 사용하는 코드입니다.

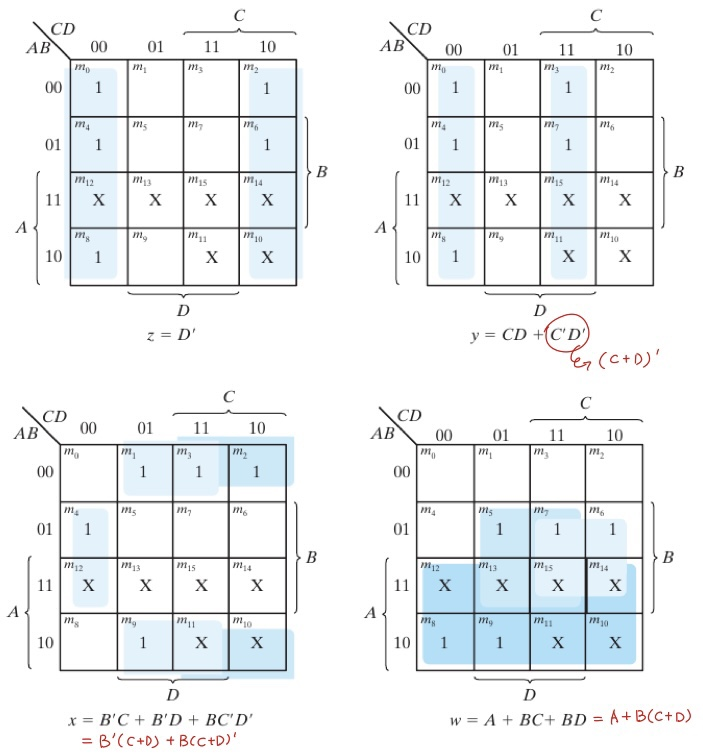
위 Truth Table를 보고 Ouput인 w, x, y, z에 대해 K-Map을 그려보면 위와 같습니다. 이때 K-Map에 Don't Care가 있는 이유에 대해 생각해보면 BCD코드는 0~9까지를 이진수로 나타냈지만 4bit으로 만들수 있는 가지수는 총 16가지 입니다. 따라서 10진수 10~15에 해당하는 숫자는 Don't Care로 처리할 수 있습니다.

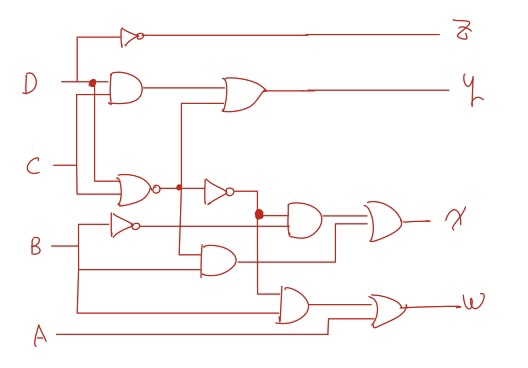
위와 같이 Gate를 사용해해 BCD를 Excess-3로 변환하는 Code Conversion 회로를 구현할 수 있습니다.

다음은 Binary Adder를 설계해보겠습니다. 우리가 1011 + 0011과 같은 연산을 수행한다고 생각해보겠습니다.

LSB부터 더하기 시작하면 1011의 LSB인 1과 0011의 LSB인 1을 더하면 sum이 0이 나오고 carry가 1이 나오는 것을 알 수 있습니다. 이렇게 LSB인 2bit을 더하는 adder를 half adder이라고 합니다. 상위 bit은 carry까지 추가하여 총 3bit을 더하는 연산을 수행해야 합니다. 이렇게 총 3bit을 더하는 adder는 full adder로 설계해야 합니다. 그렇다면 half adder부터 차례대로 구현해보겠습니다.

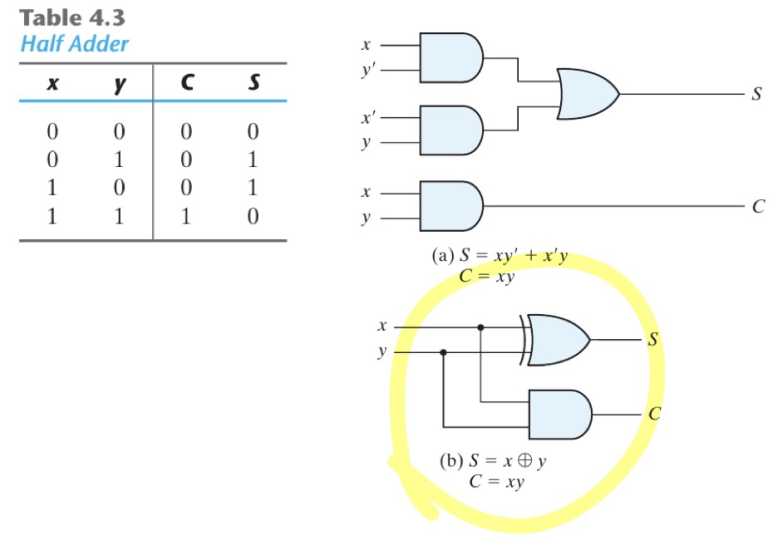
2bit을 더하는 half를 구현하면 위와 같이 XOR Gate 하나와 AND Gate 하나로 구현되는 것을 알 수 있습니다.