이번 포스팅에서는 부울 대수에 대해 알아보도록 하겠습니다.

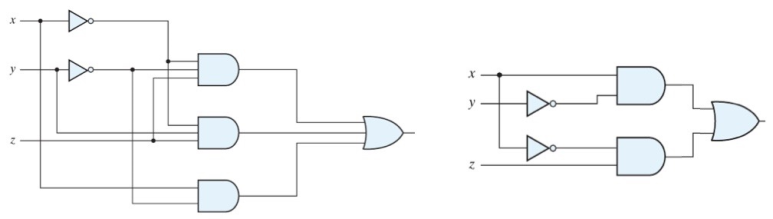
위 두 회로는 동일하게 동작하는 회로입니다. 그렇다면 어떤 회로가 잘 설계된 회로일까요? 당연히 오른쪽 게이트가 잘 설계된 회로라고 할 수 있습니다. 회로에서 Gate의 숫자가 줄어들면 Chip의 area도 작아지고 energy 효율도 좋아질 것이라고 예상할 수 있습니다. 우리는 왼쪽 회로를 오른쪽 회로처럼 설계하기 위해 부울 대수에 대해 알아야하고 이를 이번 포스팅에서 다뤄보겠습니다.

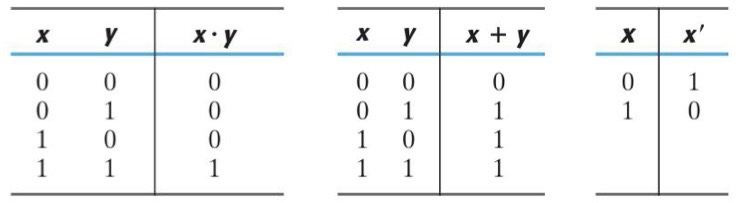
{0, 1} 두 가지 원소가 있고 +, · 두 가지 연산자가 있을 때 부울 대수는 위와 같이 정의됩니다. 즉 {0, 1} 두 가지 원소들에 대해 위와 같은 연산자로 정의된 수 체계라고 간단하게 짚고 넘어가겠습니다.

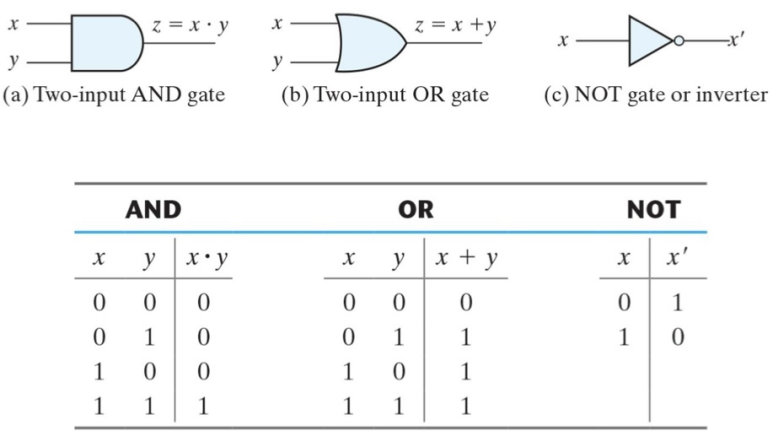
AND, OR, NOT Gate에 대해 위와 같이 정의됩니다.

위 사진은 Postulate와 Theorem에 대해 정리해놓은 것입니다. 여기서 Theorem은 Postulate를 사용해 증명이 가능합니다. 그렇다면 간단한 예제를 풀면서 Theorem을 Postulate를 사용해 증명해보겠습니다.

1(a) 와 1(b) Duality 이므로 0을 1로 ·를 +으로 바꿔 증명할 수 있습니다.

2(a)도 Postulate를 사용해 증명하고 Duality로 2(b)를 증명할 수 있습니다.

Theorem 3은 보수의 보수는 자기 자신이므로 간단하게 증명할 수 있고 6(a)와 6(b)는 Duality로 간단하게 증명할 수 있습니다.

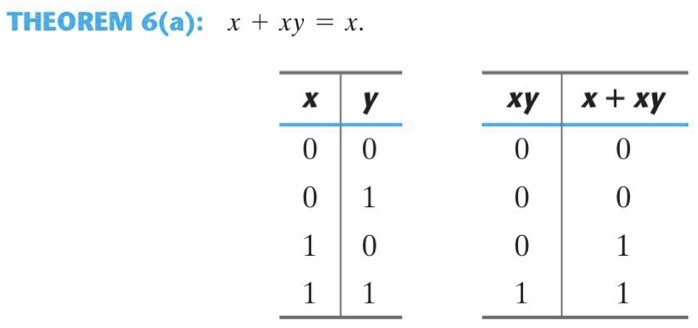
또는 위와 같이 Truth Table를 사용해 증명할수도 있습니다.

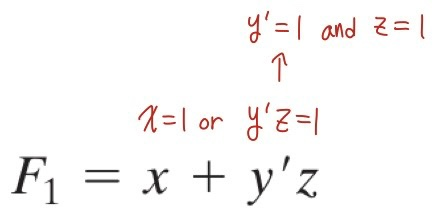
우리가 위 Boolean Function을 보면 어떻게 해석할 수 있을까요? 이것을 보고 x = 1 이거나 y'z = 1 일때 F1이 1이 되는 것을 알 수 있습니다. y'z = 1이 되기 위해서는 y' = 1 이고 z = 1 이여야 한다는 것을 알 수 있습니다. 그리고 나머지 경우에는 0인 것을 알 수 있습니다.