数据结构-图

图G（Graph）由两个集合：V（Vertex）和E（Edge）组成，记为G = (V, E)，其中V是顶点的有限集合，记为V(G)，E是连接V中两个不同顶点（顶点对）的边的有限集合，记为E(G)。结点之间的关系为多对多，任两个结点之间都可能有关系存在。例如： V(G) = {v1, v2, v3, v4, v5}

E(G) = {(v1, v2), (v1, v4), (v2, v3), (v2, v5), (v3, v4), (v3, v5)}

图的基本术语

有向图和无向图

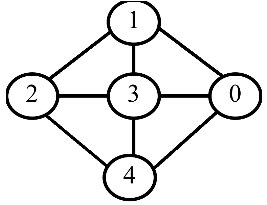
如果代表边的顶点对是无序的，则称G为无向图。

E

(

G

) = {(1, 2), (1, 3), (1, 0), (2, 3), (2, 4), (3, 4), (3, 0), (4, 0)}

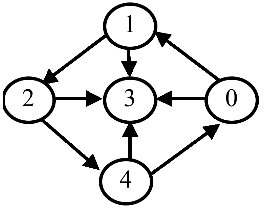
如果代表边的顶点对是

有序

的，则称

G

为

有向图

。

E