视频地址:
http://player.bilibili.com/player.html?aid=31289365&bvid=BV1iW411d7hd&cid=60026257&page=2
http://player.bilibili.com/player.html?aid=31289365&bvid=BV1iW411d7hd&cid=65793335&page=3
课件地址:
对应于书本的2.1~2.3。
如有错误请指出,谢谢。
小点:
模运算相当于忽略某些位的值,比如计算x mod 8,则只保留x低三位的值。
比较有符号数和无符号数之间的大小,先将其转化为二进制编码,再根据特定编码计算比较。
所有性质都可以直接通过二进制以及对应的编码去解释,首先考虑二进制的值是什么。
补码和无符号数对应的位向量,在计算结果上都是相同的,大部分计算机中使用相同的机器指令进行计算,所以可以。
先将补码转换为无符号数进行推导,再转为补码会更容易
加法逆元的求法就是通过溢出实现的,比如求x的加法逆元,直接计算~x+1,就能保证有效位里都是0。
尽量不使用无符号数。
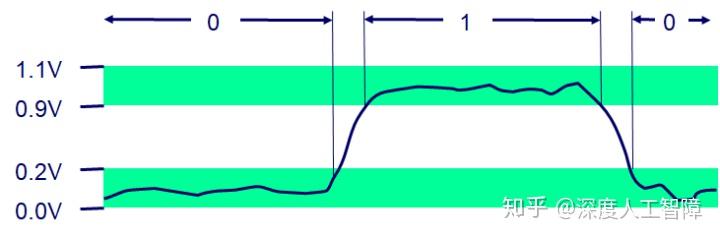
现代计算机存储和处理的信息是以二值信号表示的,是基于二进制进行编码的,**好处在于:**1. 比如我们可以将低电压表示0,将高电压表示1,如果电路中存在噪音或不完善的地方,只要不超过你设定的阈值,你就会得到一个清晰的信号;2. 对于信息存储而言,存储一位信息或一个数字值比存储一个模拟值更容易。

当我们将若干个二进制数组合在一起,再加上某种解释,就能给这些二进制数赋予特定的含义,这个“解释”就是编码。比如对于文档中的字符和符号,我们可以使用标准的字符码将二进制数与字符和符号对应起来;对于数字表示,我们可以使用无符号编码来表示大于或等于零的数字,可以使用补码来表示有符号整数,可以使用浮点数编码来表示数字的科学计数法。
由于浮点数和整型数使用不同的编码规则,所以即使他们存储相同的数字,可能二进制序列也不相同。