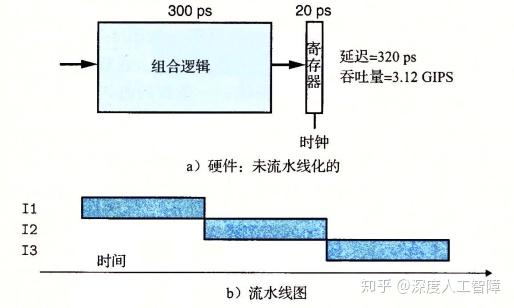

如上图所示是一个非流水线化的计算硬件。当信号输入到组合逻辑中时,通过一系列逻辑门经过300ps获得输出信号,然后经过20ps将结果加载到寄存器中,由于时钟周期控制存储器写入的频率,为了保证当时钟变为高电平之前,能够得到将计算好的结果放到寄存器的输入端口,则这里的时钟周期设定为300+20=320ps。
我们将从头到尾执行一条指令所需的时间称为延迟(Delay),则这里延迟为320ps。我们将系统在单位时间内能执行的指令数目称为吞吐量(Throughput),则
$$ \text { Throughput }=\frac{1 I}{320 p s} \cdot \frac{1000 p s}{1 n s}=3.12 G I P S $$
意味着一秒能执行3.12G条指令。
由于这个是非流水线化的计算硬件,所以从流水线图中可以看到在开始下一条指令之前必须完成上一条指令。如果我们将组合逻辑根据不同功能,通过**流水线寄存器(Pipline Register)**划分成独立的三阶段,就能得到简易的流水线化计算硬件。
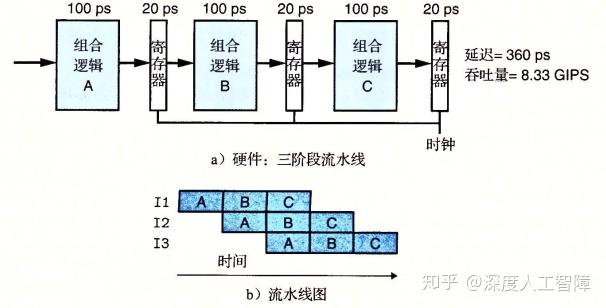
由于每阶段的组合逻辑实现独立的功能,并且能通过流水线寄存器来控制进入下一阶段的时机,所以如上图的流水线图所示,只需要通过流水线寄存器控制每个阶段只执行一条指令,就能流水线化地执行指令。
对于每个阶段,我们需要100ps的组合逻辑计算时间以及20ps加载到寄存器的时间,所以我们这里能将时钟周期设定为120ps。并且我们可以发现每过一个时钟周期就有一条指令完成,所以吞吐量变为了8.33GIPS,提高了2.67倍。但是每条指令需要经过3个时钟周期,所以延迟为360ps,变为原来的1.12倍。
所以流水线特点为:提高系统的吞吐量,但是会轻微增加延迟。
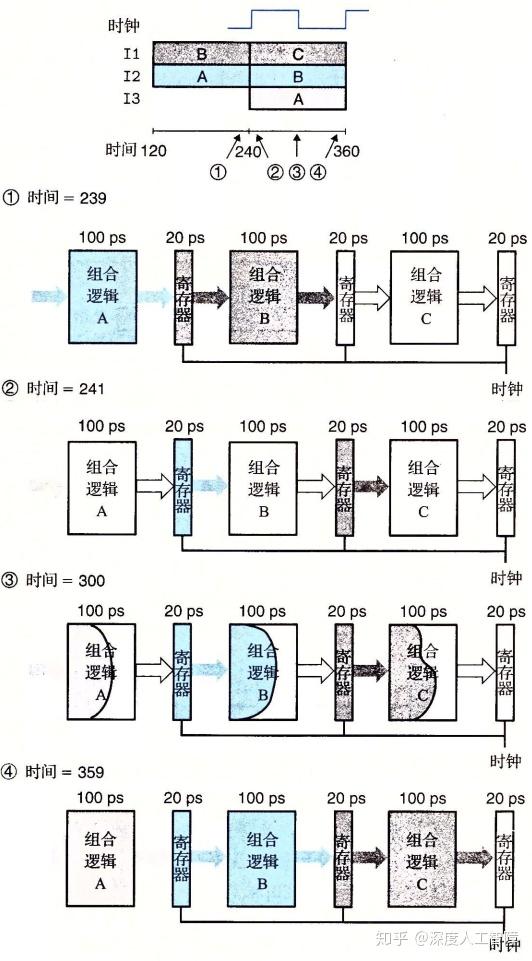
上图是其中一段时间详细过程。
I2经过组合逻辑A的计算到达寄存器A,I1经过组合逻辑B的计算到达寄存器B,此时时钟还处于低电平,则流水线寄存器还未读取组合逻辑计算的结果,还保持着原来的值。I2在组合逻辑A中计算的结果,寄存器B保存I1在组合逻辑B中计算的结果。**时钟周期的影响:**时钟周期用来控制流水线寄存器的读取频率,用来将不同阶段分隔开来,互不干扰。如果时钟周期太快,组合逻辑的计算还未完成,就会使得非法的值保存到寄存器中。如果时钟周期太慢,不会导致计算错误,只是效率会比较低。